ADP 기출문제 풀이) 탐색적 분석 관련 문제들 w/Python
예전부터 기출문제 풀이 관련 포스팅을 해보려고 생각만 하고 있었는데, 드디어 ADP 실기 기출문제에 대한 포스팅을 시작해본다.
ADP와 빅분기를 준비하는 분들이 많이 사용하고 있는 데이터마님 사이트(https://www.datamanim.com/)에서 복원해놓은 문제들을 내 방식대로 풀어보고자 한다.
나의 풀이가 만점짜리 풀이가 아닐지라도 누군가에게는 참고와 도움이 되기를 바라면서^^
(내용 상 오류나 질문들은 댓글로 달아주시면 대환영입니다)
ADP 실기 기출문제 풀이 포스팅 시작 !
1. 학생특성과 결석 빈도 데이터 (ADP 실기 24회)
성별(sex) 바이너리 : ‘F’ - 여성 또는 ‘M’ - 남성
나이(age) 숫자: 15 - 22
부모님동거여부 (Pstatus) 바이너리: T: 동거 또는 ‘A’: 별거
엄마학력(Medu) 숫자 : 0 : 없음, 1 : 초등 교육, 2 : 5-9학년, 3 - 중등 교육 또는 4 - 고등 교육
아빠학력(Fedu) 숫자 : 0 : 없음, 1 : 초등 교육, 2 : 5-9학년, 3 - 중등 교육 또는 4 - 고등 교육
주보호자(guardian) 명목형 : ‘어머니’, ‘아버지’ 또는 ‘기타’
등하교시간(traveltime) 숫자 : 1 : 15분이하, 2 : 15 - 30분, 3 : 30분 - 1시간, 4 : 1시간 이상
학습시간(studytime) 숫자 : 1 : 2시간이하, 2 : 2-5시간, 3 : 5-10시간, 4 : 10시간이상
학고횟수(failures) 숫자 : 1, 2, 3 else 4
자유시간(freetime) 숫자 : 1(매우 낮음), 2, 3, 4, 5(매우 높음)
가족관계(famrel) 숫자 : 1(매우 나쁨), 2, 3, 4, 5(우수)
[출처] https://www.datamanim.com/dataset/ADPpb/00/24.html

# 1-1. 다음 데이터를 탐색적으로 분석하고 시각화 하시오.
데이터는 총 12개의 변수로 되어 있는데 이 중, absenses는 타겟변수, 나머지는 예측변수로 판단된다. 데이터 크기는 395개인데, age, traveltime, freetime는 소수의 결측치를 가지고 있다. 데이터 타입과 컬럼 정의서를 근거하여 판단해보면, age와 absences는 양적 변수, 나머지 변수들은 범주형 변수로 볼 수 있다. 비록 어떤 변수들(Fedu, Medu, studytime, traveltime, failures, famrel, freetime)은 수치로 되어 있어서 양적 변수처럼 보이지만 범주형 변수이며 이중, Medu, Fedu, traveltime, studytime, failures, freetime, famrel은 순서의 정보를 가지는 순위변수이다.

수치형 변수인 age와 absences의 기술통계는 다음과 같다. age의 데이터 개수는 392개이고, 평균값은 16.7이며, 표준편차는 1.28, 최솟값과 최댓값은 각각 15, 22이고, 1/2/3사분위수는 각각 16, 17, 18이다. absences의 데이터 개수는 395개이고, 평균값은 5.71이며, 표준편차는 8, 최소값과 최댓값은 0, 75이고, 1/2/3사분위수는 각각 0, 4, 8이다.

범주형 변수들의 데이터 타입을 'category'로 변경한 후, 아래와 같이 기술통계 결과를 얻었다. 각 데이터의 개수와 수준의 개수(unique), 빈도가 가장 많은 수준(top)과 그 수준의 빈도(freq)를 아래와 같이 확인할 수 있다. 모든 변수들이 5개 이하의 수준을 가지고 있으며, 수치로 표현된 Fedu, Medu, studytime, traveltime, failures, famrel, freetime의 변수들은 순서 정보도 포함하고 있다.

양적변수와 질적변수의 데이터 시각화 방법은 차이가 있기 때문에 아래와 같이 각각 시각화를 진행하고자 한다. 먼저 양적변수인 age, absences에 대하여, 히스토그램, 상자그림을 통해 시각화한 결과는 다음과 같다.
age와 absences의 히스토그램을 통해 두 데이터 모두 데이터가 왼쪽으로 쏠려 있고, 오른쪽 꼬리를 가지는 형태의 데이터를 가짐을 알 수 있다. 왜도와 첨도를 살펴보면, 정규분포의 왜도가 0, 첨도가 3인 것과 비교해볼 때, age는 왜도 0.46, 첨도 -0.02이고 absences는 왜도 3.67, 첨도 21.72임을 알 수 있다.
age와 absences의 상자그림을 통해 두 변수 모두 이상치를 가지고 있음을 확인하였고, 특히 absences의 경우, 비교적 범위가 넓으며 중앙값과 이상치의 차이가 매우 큼을 알 수 있다.


질적변수들은 막대 그래프와 파이 그래프로 시각화 할 수 있으며 그 결과는 다음과 같다.

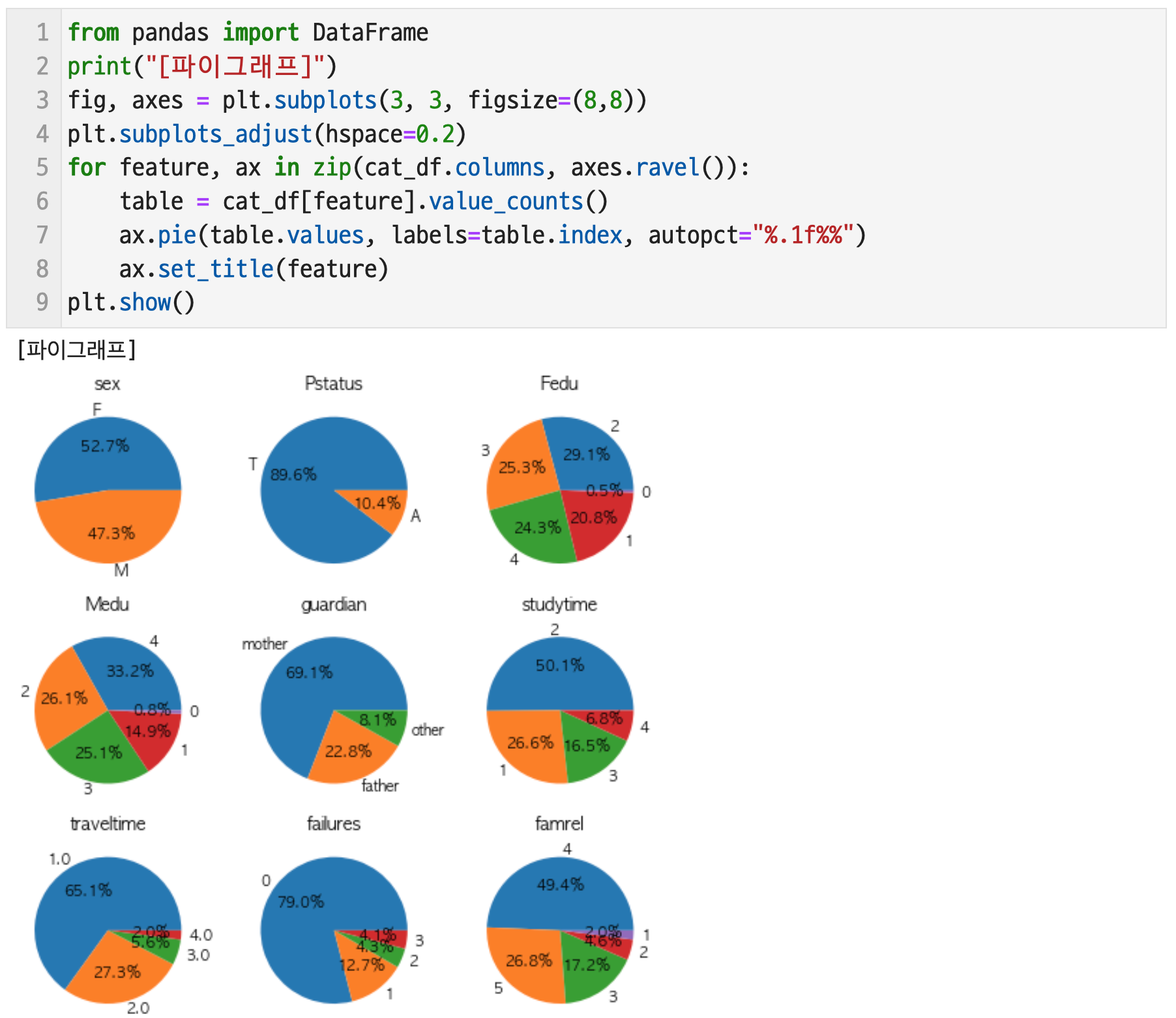
# 1-2. 다음 데이터의 결측치를 처리하고 그 변화를 시각화 하시오. 추가적인 전처리가 필요하다면 그 전처리에 대한 설명과 이유, 기대효과를 설명하시오.
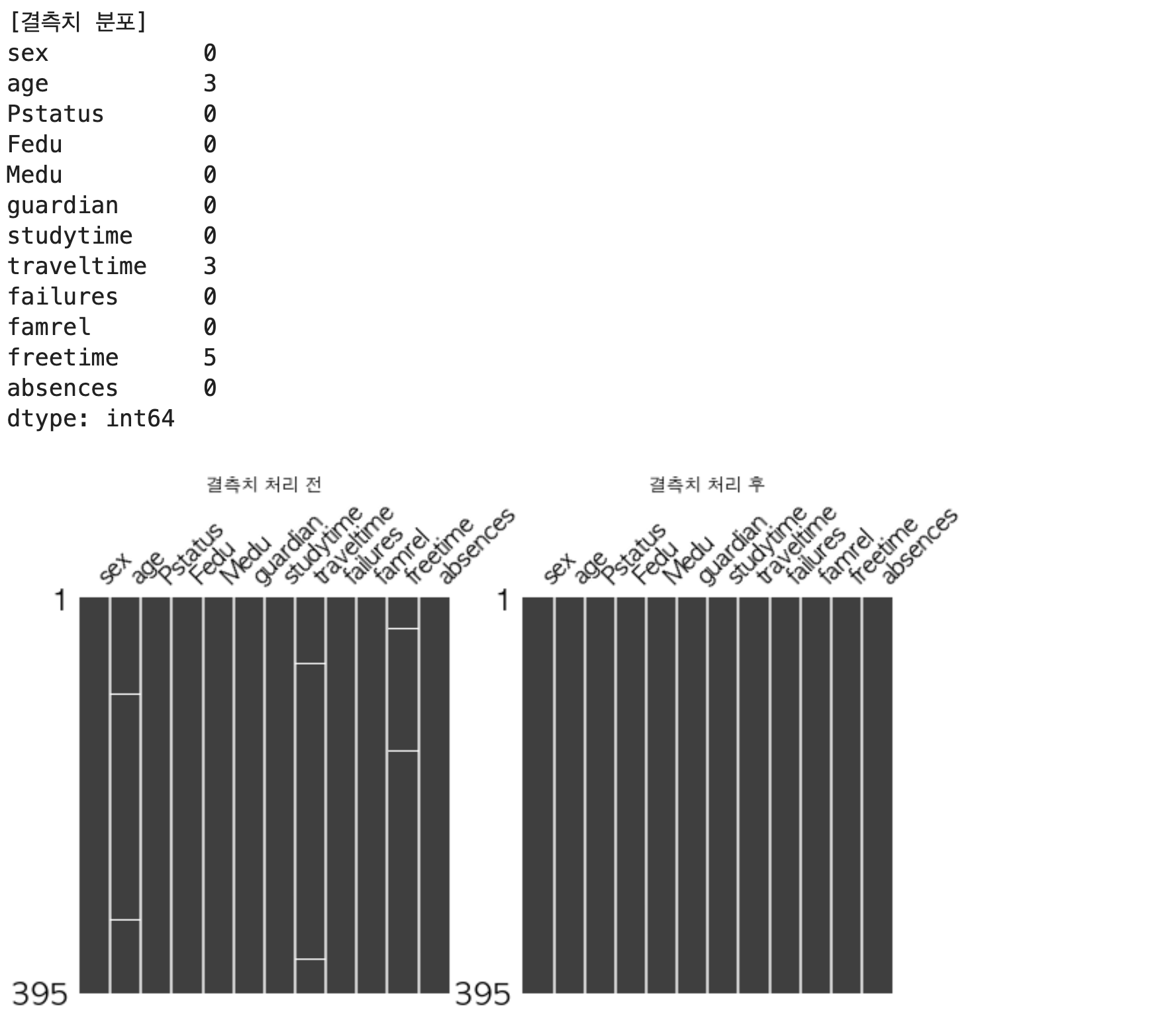
결측치를 갖는 feature는 age, traveltime, freetime이다. 세개의 변수 모두 대푯값으로 채우는 방법으로 결측치를 처리하고자 한다. 양적변수인 age는 평균값으로, 질적변수인 traveltime과 freetime은 최빈값으로 결측치를 채우고자 한다.
missingno 라이브러리로 아래와 같이 결측치 처리 전(df)과 처리 후(imp_df)의 데이터를 시각화할 수 있으며, 처리 후의 그래프에서는 결측치가 없는 것으로 확인된다.
추가적인 전처리로 absences의 이상치를 처리하는 방법이 있다. 이상치가 있으면 변수들 사이의 보편적인 관계가 왜곡되어 잘못된 학습 결과를 얻을 수 있기 때문이다. 이상치를 처리하는 방법으로는 극단값을 절단하는 방법, 조정, 클리핑 등이 있는데, 해당 경우에는 데이터 크기가 작기 때문에 데이터 소실을 막기 위해 조정의 방법이 가장 적합할 것으로 생각한다.

2. 객실 특성과 객실 사용유무 판별 데이터 (ADP 실기 23회)
Occupancy: 0 - 비어있음, 1 - 사용중
[출처] https://www.datamanim.com/dataset/ADPpb/00/23.html
# 2-1. 데이터에 불균형이 있는지 확인하고, 그렇게 생각한 이유를 작성하시오.
해당 데이터는 불균형이라고 할 수 있다. 데이터 불균형이란 타겟변수의 클래스 수가 불균형한 데이터 상황을 뜻하는데, 본 데이터의 타겟변수인 Occupancy의 클래스 비율을 살펴보면 아래와 같이 88% : 12%로 차이가 많이 나기 때문이다.

# 2-2. 오버샘플링 방법들 중 2개를 선택하고 장단점과 선정 이유를 작성하시오.
불균형 데이터를 처리하기 위한 오버샘플링 방법들에는 랜덤오버샘플링, SMOTE, Borderline SMOTE, K-means SMOTE, SVM SMOTE, ADASYN이 있다. 그 중에서도 imbalanced-learn을 통해 간단히 오버샘플링할 수 있는 효과적인 방법인 랜덤오버샘플링과 SVM SMOTE를 선택하고자 한다.
랜덤오버샘플링은 기존에 존재하는 소수의 클래스를 단순 복제하여 클래스가 불균형 하지 않도록 비율을 맞춰주는 방법이다. 분포의 변화는 없으나 소수 클래스의 숫자가 늘어나기 때문에 더 많은 가중치를 받게 되어 유효하다고 본다. 예측변수가 질적변수이거나 결측치가 있어도 전처리가 필요없다. 반면, 과적합의 위험이 있다.
SVM SMOTE는 SVM 알고리즘으로 데이터를 학습함으로써 생성되는 support vector 데이터들 중에서 소수 클래스 데이터들을 경계 데이터로 삼아 SMOTE를 적용하는 방법이다. 이 때문에 support vector로서 유효한 소수 클래스 데이터들이 오버샘플링된다는 장점을 가진다. 반면, 데이터를 학습해서 생성해야 하기 때문에 랜덤오버샘플링보다는 시간이 좀 더 걸릴 수 있고, 예측변수들의 값이 모두 수치형이어야 하고, 결측값이 없어야한다는 단점이 있다.
# 2-3. 오버샘플링 수행 결과, 잘 되었다는 것을 판단하시오.
예측변수 내 결측치를 평균값으로 대치하고, 질적변수인 date를 제거한 후 오버샘플링을 진행한다. 앞서 불균형이었던 타겟변수의 클래스가 동일하게 오버샘플링된 것을 확인할 수 있다.
