파이썬) statsmodels로 logit함수 이해하기 (+Logit Regression Results 해석)
#1. logit함수값과 오즈비는 무엇인가?
statsmodels패키지를 설치하면 from statsmodels.formula.api import logit을 통해 logit 함수를 사용할 수 있다.
logit함수값을 구하기 위해서는 logit('종속변수명 ~ 독립변수명1 + 독립변수명2 + 독립변수명3', data=데이터프레임객체).fit().summary() 의 형태로 코드를 구성하는데, 아래와 같이 그 결과값들을 확인할 수 있다.
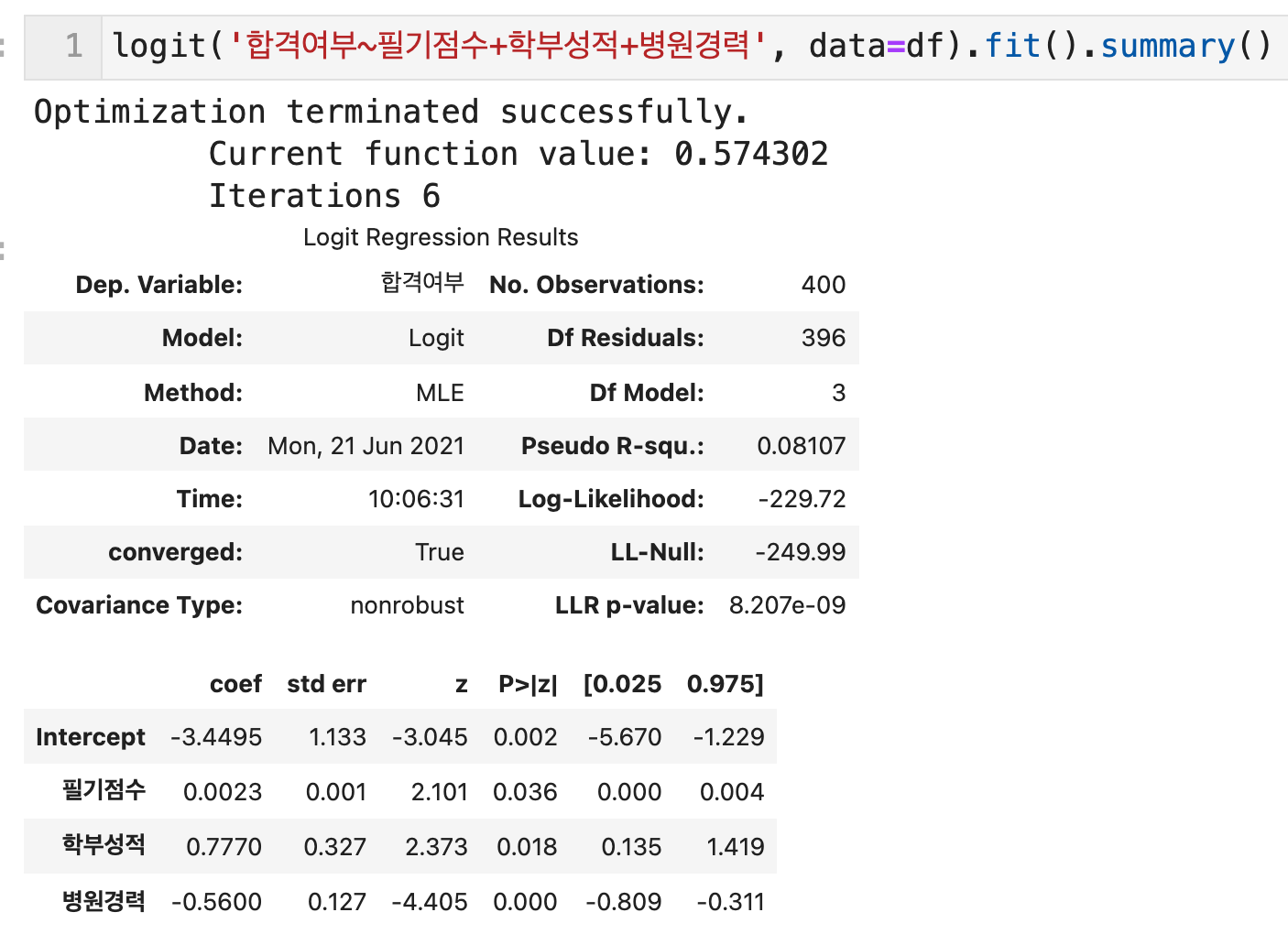
이중에서 맨 아래에서 coef가 바로 각 독립변수들의 logit함수 계수들이다. 해당 값이 0에 가까울수록 종속변수에 미치는 영향이 적고, 해당 값이 0에서 멀수록 종속변수에 영향력이 있다고 볼 수 있다.
로짓함수식에서 Intercept는 절편이고, coef는 해당 독립변수의 오즈비에 log를 씌운 값이다. 즉 log(오즈비)이다. 참고로 여기서 log는 상용로그가 아니라 자연상수 e에 대한 로그이다. 또한, 오즈비는 실패할 확률 분의 성공할 확률이고, 아래에서는 합격여부가 종속변수이므로 불합격할 확률 분의 합격할 확률이다.
#2. 오즈비(Odds ratio)를 확인하려면? -- logit함수의 계수를 지수함수로 변환한다
위에서 전체 summary()형태의 결과값 말고, 아래 코드를 통해 각 logit함수의 계수들을 하나의 array로 받아 올 수 있다.
logit('종속변수명 ~ 독립변수명1 + 독립변수명2 + 독립변수명3', data=데이터프레임객체).fit().params
이 array에 np.exp( )를 씌우면 각각의 회귀계수들을 밑이 자연상수 e인 지수함수(e^회귀계수값)로 변환할 수 있다. 즉, np.exp( logit값 ) = 오즈비 를 구하는 것이다.

오즈비를 보면, 해당 독립변수가 종속변수에 미치는 영향을 더 직관적으로 확인할 수 있다. 학부성적의 경우, 오즈비가 2 정도 되는데 합격확률이 불합격확률의 2배라는 것을 보아 종속변수인 합격여부에 끼치는 영향이 크다고 볼 수 있다.
#3. 로지스틱 회귀식 구하기
파이썬의 로지스틱 모델을 통해 자동예측값을 얻으려면, 각 독립변수에 값을 아래와 같이 입력하면 된다.
logit('합격여부~필기점수+학부성적+병원경력', data=df).fit().predict({'필기점수':380, '학부성적':3.61, '병원경력':3})
그러면, 합격확률을 예측해준다. 이 결과값이 0.5 이상이면 합격, 0.5미만이면 불합격으로 예측해준다.
수기로 로지스틱 함수 식을 만들어서 비교해보았다. 일단 로지스틱 함수와 로짓함수의 관계를 보면 아래와 같다.
logistic(z) = 1 / 1+exp(-z)
z 는 앞선 logit regression summary에서 확인한 계수들을 독립변수들과 곱해서 더한 값에 절편까지 더한 식이다.
z = x1 * logit계수 + x2 * logit 계수... + 절편
이에 따라 수기로 만든 logistic 함수식은 아래와 같다.
1 / (np.exp( -( 앞선 summary에서 받은 logit 계수들과 독립변수를 곱하여 더함 + 마지막으로 절편도 더함 ) + 1 )

위의 코드 실행 결과에서 보듯이, logit().predict를 통해 한 예측값과 수기로 만든 logistic 함수식을 계산한 결과값이 동일한 것을 확인하였다.